近日，实验室2篇论文被AAAI-24接收。AAAI Conference on Artificial Intelligence会议是人工智能领域最重要的国际会议之一，是CCF A类推荐会议，每年举办一届。AAAI-24将于2024年2月22-25日在加拿大温哥华举行。本次AAAI-24共有9862篇投稿，录用2342篇，录用率23.75%。

1、Diversity-Authenticity Co-constrained Stylization for Federated Domain Generalization in Person Re-identification

近年来，借助联邦学习在保护数据隐私的同时提升模型泛化引起了学界广泛的关注。本文致力于通过图像风格迁移来解决行人重识别中的联邦域泛化问题，通过设计风格迁移模块丰富每一个终端的数据风格用于模型训练，从而在保护数据隐私的同时提升模型泛化。具体而言，该模型将图像风格抽象为两个可训练的风格向量，为了在联邦约束下高效搜寻有效的风格向量，本文分别提出多样性与真实性损失来控制风格向量的优化过程。多样性损失通过要求风格向量与本地风格向量不同来提升数据多样性，真实性损失则通过对比局部模型与全局模型之间的预测置信度来定义真实性，并作为额外约束进一步控制风格向量的优化。在大量数据集上的实验证明了该方法在联邦域泛化领域的有效性。

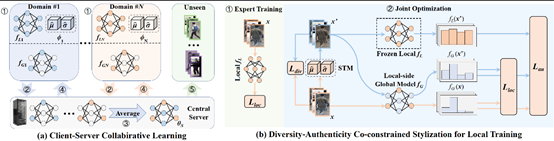
该论文第一作者是实验室博士生杨丰祥，通讯作者是实验室罗志明副教授，合作者还有实验室李绍滋教授、诺丁汉大学钟准教授、意大利Trento大学Nicu Sebe教授和瑞为科技何一凡博士。

2、An Interpretable Approach to the Solutions of High-Dimensional Partial Differential Equations

求解偏微分方程对于模拟现实世界，理解物理、工程和金融等领域中的现象具有重要意义。近年来，机器学习算法，特别是深度学习，在求解偏微分方程(PDEs)方面显示出了良好的前景。然而，随着维数的增加，变量之间的关系和相互作用变得更加复杂，现有方法难以快速为高维偏微分方程提供可解释的结果。为了解决这一问题，本文提出了一种基于迁移学习和自动微分的遗传规划符号回归算法来求解偏微分方程。该方法利用遗传规划寻找数学上可理解的表达式，并结合自动微分来判断搜索结果是否满足待解的偏微分方程和边界条件。所提出的迁移学习机制将一维偏微分方程解析解的结构转化为高维偏微分方程解的形式，以克服高维问题搜索空间大导致的求解速度慢的问题。在三种典型的偏微分方程上的实验，证明该方法能够得到可靠且易于理解的偏微分方程的解析解或代数等价解，且收敛速度优于对比方法。

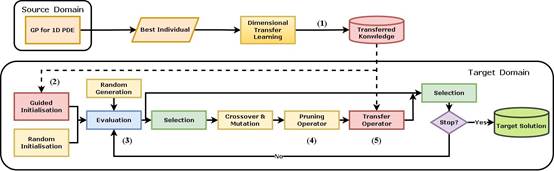
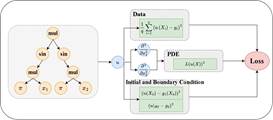
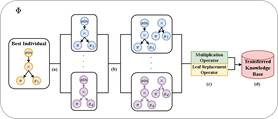
该论文第一作者是实验室硕士生曹璐璐，通讯作者是实验室江敏教授，合作者还有香港理工大学Kay Chen Tan教授、博士生王贞众等人。